1. How it began

Face down on the linoleum ...
In 1990 I made my second annual trip to the International C++ Users Group meeting. On the return trip I stopped by to see my parents for a few days. I spent most of my time there recovering from a virus that no doubt was a gift from the close quarters that conventions provide and the shared food in all those incubating buffets.
I had repeated opportunities to closely examine the pattern of the linoleum in the old bathroom, and I have no doubt the free stock photo here accurately represents my field of view for two or three days that Fall. I blurred my eyes, crossed them (sometimes intentionally) and gradually associated this repetitive pattern with the hourly recurring pattern of my illness. It must have been a popular print in linoleum because it was used in a different color scheme on the kitchen floor of a house my parents owned in the early 1960s.
The building

In 1993 I went to Australia on general business and to give a paper at the CHI conference. With no associated convention maladies, I had my first encounter with the Penrose tiles in the wild. The picture to the left (sourced from Wikipedia) is of the Storey Hall façade at RMIT.
I had first learned of the Penrose tiles in the article in Scientific American where they were discussed in 1977. The hope of a non-repeating but highly organized pattern for tiling has stayed with me since that time. But pentagonal symmetry is not something that would come easily to flooring manufacturers.
The Quilts
There are quilts done with the Penrose tiles, but they tend to be less useful than rectangular quilts when it comes to fitting the bed. Rectangular quilts tend to be square tiled affairs, although the squares themselves are often ornate, unique, and even arranged to tell something of a history of the quilter. For a tiling pattern to work for quilts, it almost must be made of rectangles if there is to be an advantage to be had from machine sewing.
To my practiced bedtime eye, the most interesting pattern would be one that neatly covered the horizontal surface of the bed, and with a barely discernable, non-repeating design. The same could be said of the floor for a small room, the tiles of a patio, or even the layout of a cork board made with wine bottle corks.
Along came Knuth
If you have been reading along with Dr. Knuth's output for the past forty years, then you probably know that Part 1 of Volume 4 of The Art of Computer Programming was published about two years ago. I started on it this summer.
Knuth discusses another fascination of mine, gray codes, in his usual level of ultra-condensed detail. I began to think of how tiles or parquet laid in the pattern of a gray code might look down a long hall or even in an entry way. Quilts and more colorful tilings could be made from multi-bit gray codes, but a few hand colored examples convinced me that I should keep looking.
My wife recently bought me Knuth's Selected Papers on Fun and Games, and the newest addition to my reading material has brought me to my latest plateau in my quest for almost-non-repeating tiling patterns that can be easily cut, sewn, grouted, laid, fired and all those other steps of mechanization that are required.
After all, with any patio, or quilt, or floor, or side of a building ... the surface is finite, and all that is really needed is a pattern on the surface that exactly fills it once without repeating.
And Elliott Carter
Elliott Carter died this year (2012) a couple of months short of his 104th birthday. Consider what this means to one's life span; Beethoven died at 56 and still managed to have early, middle and late periods, the latter two separated by several years of inactivity. In 1964 Carter turned 56 and went on to have very late, late late, and second childhood periods.
Like some other people in the second half of the previous century, Carter experimented with long-period rhythms he created by dividing the musicians into groups that are to play in contrasting time signatures. Periodically, the rhythms coincide (or ''collide'' if you prefer). Listening to the music, you begin to anticipate the arrival of the next dual or triple down-beats without necessarily being able to count the time for each group of musicians.
More about this in a bit.
2. Putting it together
Knuth's Leapers
Fun and Games includes a chapter on Leapers. Leapers are a species of fantasy chess piece that move point-to-point much like a knight.
Leapers jump around at distances other than the one square in one direction and two in the
other, and the boards can be something other than 8 x 8 squares. The graphic shown here
is from a Wikipedia article, and shows a regular knight moving on a 5 x 5 board, visiting
each square in turn.

The chapter on Leapers concerns itself with what properties the combination of Leaper move and board size must have for the leaper to be able to get to all the squares. Some of the properties are obvious: the components of the leaper's move cannot both be odd or both be even, and the leaper's move cannot be so large than the middle of the board is unreachable. Other restrictions are more subtle.
Knuth spends most of his chapter discussing the theory of the metric space created by super-boards and super-knights. At the end of the chapter is an Addendum, and those of us who are regular readers of Knuth have noticed that it is in these appendices that we often find the most interesting ideas.
There are ample opportunities for research. In particular, Fibonacci Leapers (5x8), (8x13) on boards just big enough will probably make interesting patterns.
Here then is the opportunity to have a structured, but non-repeating tiling pattern
made entirely from squares --- which is to say, easily cut, easily joined or sewn pieces of
material requiring no special manufacturing equipment to produce.
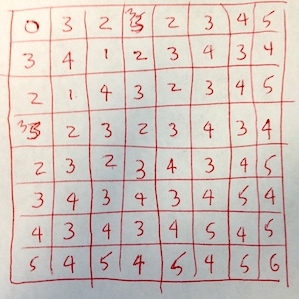
My experiment in working out the pattern by hand convinced me that it was impractical. Shown here without too much embarrassment is my attempt to transcribe the case for the usual chess knight and the ordinary 8 by 8 board. As you can see, I only got to ''3'' before I made my first mistake. This result sealed the deal that programming would be required if I were to correctly cover a 31 x 19 patio with tiles.
The first program: leaper.cpp
In the past two decades I have written a little C++, and like most people with an axe, I turned first to it. I wrote a short program to check for connectedness, and assuming that test passed, fill in the distances with numbers and letters associated with the number of leaps required from the upper left corner. My first attempt for that 31 by 19 patio using a 8 over 9 across leaper is shown here, using 0-9 followed by A-Z to cover distances up to 35 units.
leaper 8 9 19 31 Max distance in graph 19 0 H 4 H 8 H C H G H E H A H 6 H 2 H 2 H 6 H A H E H G H C H 8 H 4 H 6 F A F E F G F C F 8 F 4 F 2 H 4 F 8 F C F G F E F A F 4 H 6 F 8 D C D G D E D A D 6 D 4 H 4 F 6 D A D E D G D C D 8 H 6 F 8 D A B E B G B C B 8 B 6 F 6 F 6 D 8 B C B G B E B A B 8 F 8 D A B C 9 G 9 E 9 A 9 8 D 8 H 8 D 8 B A 9 E 9 G 9 C 9 A H A D A B C 9 E 7 G 7 C 7 A B A F A F A B A 9 C 7 G 7 E 7 C 9 C F C B C 9 E 7 G 5 E 5 C 9 C D C H C D C 9 C 7 E 5 G 5 E 7 C H E D E 9 E 7 G 3 G 3 E 7 E B E F E F E B E 7 E 5 G 3 G 5 E 9 G F G B G 7 G 3 I 1 G 5 G 9 G D G H G D G 9 G 5 G 3 I 3 G 7 G H G D G 9 G 5 G 1 I 3 G 7 G B G F G F G B G 7 G 3 G 3 I 5 G 9 E F E B E 7 E 3 G 3 G 5 E 9 E D E H E D E 9 E 5 E 3 I 5 G 7 E H C D C 9 C 7 E 5 G 5 E 7 C B C F C F C B C 7 C 5 G 5 G 7 E 9 A F A B A 9 C 7 G 7 E 7 C 9 A D A H A D A 9 A 7 E 7 G 7 E 9 C H 8 D 8 B A 9 E 9 G 9 C 9 A B 8 F 8 F 8 B 8 9 C 9 G 9 E 9 C B 6 F 6 D 8 B C B G B E B A B 8 D 6 H 6 D 6 B A B E B G B C B A H 4 F 6 D A D E D G D C D 8 D 6 F 4 F 4 D 8 D C D G D E D A D 2 H 4 F 8 F C F G F E F A F 6 F 4 H 2 F 6 F A F E F G F C F 8 J 2 H 6 H A H E H G H C H 8 H 4 H 2 H 4 H 8 H C H G H E H A H 2 H 4 F 8 F C F G F E F A F 6 F 2 H 4 H 6 F A F E F G F C F 8 Census of distances -------------------------------------------------------------------------------- 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 9 12 16 17 22 28 31 36 40 39 49 44 57 62 65 53 5 1 Mean distance: 11.6672
My wife is often my only available audience, so I put my iPad in her field of vision with the results you see above. I explained that each letter might represent the color of a tile, or a square of fabric. Glenda understood but she was unimpressed. `But what would it look like?'
Hmmm... Yes, I was also wondering that, but I was too enthusiastic about
the early results to stop and develop a visualization. To get a quick-and-dirty look at the
possibilities, I pulled the output you see above into
vi and
searched for all the 'G' characters. Doing so caused them to appear in
reverse video.

I tried this technique with several other of the higher count letters, and
discovered that the patterns move like waves through the space in a way that
is familiar to those of us who have experimented with
John Horton Conway's cellular automaton.
For example, here is 'H', the step just after the 'G' shown above.

At the moment, this is my slightly better visualizer.
... to be continued ...